视频：
（轻微编辑）幻灯片：//www.gqpatrol.com/files/Factored-Set-Slides.pdf
（第1部分，标题幻灯片）···有限因素套装
（第1部分，动机）··一些背景
斯科特：所以我想从一些背景开始。对于不熟悉我的工作的人:
- 我的主要动机是降低存在的风险。
- 我试图通过试图弄清楚如何做到这一点对齐先进的人工智能。
- 我努力做到这试图成为不那么困惑关于智能和优化和机构以及该集群中的各种事物。
- 我这里的主要策略是制定一种代理理论嵌入式在他们优化的环境中。我认为这样做有很多打开的艰难问题。
- 这让我做了一堆奇怪的数学和哲学。这个谈话将成为一些奇怪的数学和哲学的一个例子。
对于那些是已经熟悉我的工作，我只是想说根据我的个人美学，这个谈话的主题就像令人兴奋逻辑归纳也就是说，我真的很兴奋。看到这些观众，我真的很兴奋;我很高兴现在能做这个演讲。
（第1部分，目录）···要修理谈话
这个演讲可以分为两部分:
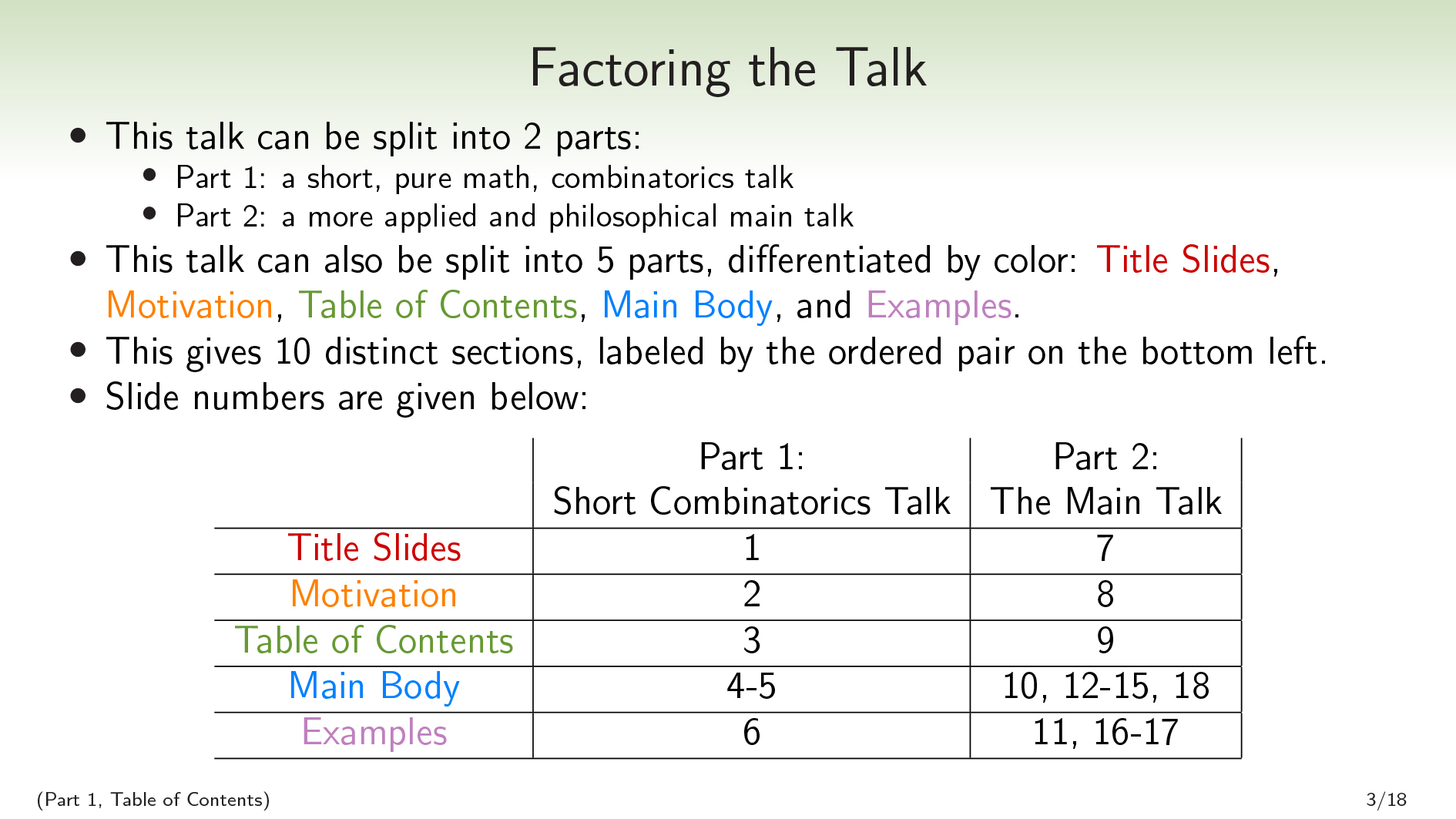
第1部分，简短的纯数学组合谈话。
第2部分，一个更实用和哲学的主要谈话。
这个谈话也可以分裂5.零件用颜色差异：标题幻灯片那动机那目录那主体， 和例子．结合这些给我们提供了10个部分（其中一些不连续）：
| 第1部分：短暂的谈话 | 第2部分：主要谈话 | |
| 标题幻灯片 | 有限因素套装 | 主谈（这是关于时间） |
| 动机 | 一些背景 | 珍珠范式 |
| 目录 | 要修理谈话 | 我们可以做得更好 |
| 主体 | 设置分区， 等等。 | 时间和正交性， 等等。 |
| 例子 | 枚举因素 | 生命的游戏， 等等。 |
(第一部分，主体)···设置分区
好吧。这是一些背景数学：
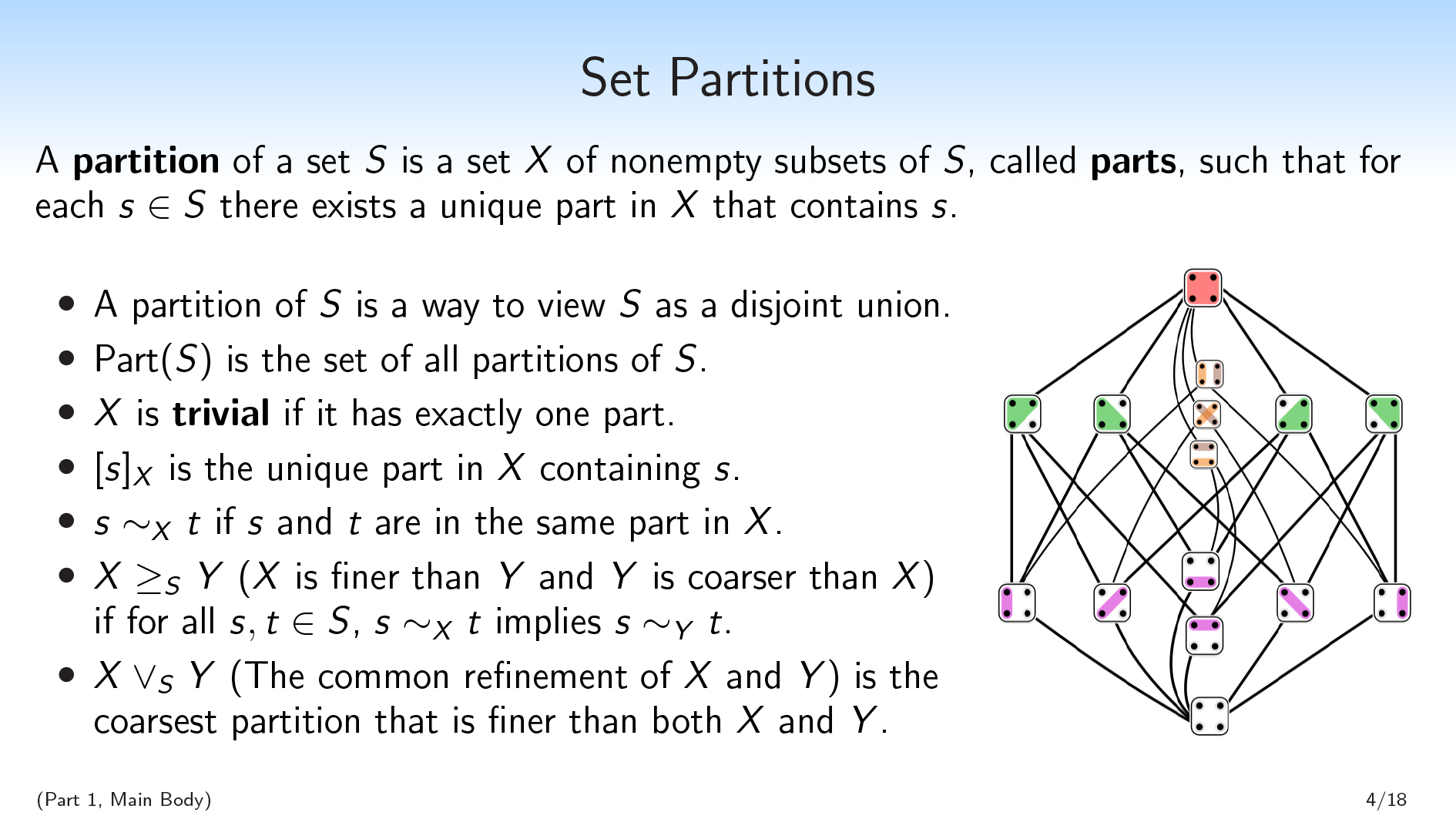
- 一种划分一个集合\（s \）是\（s \）的非空子集的集合\（x \），调用部分，例如，对于每个\（s∈s\），存在包含\（s \）的唯一部分。
- 基本上，\（s \）的分区是将\（s \）视为不相交的联盟的方法。我们有彼此不相交的部件，他们将联合在一起形成\（s \）。
- 我们将为\（s \）的所有分区集编写\（\ mathrm {part}（s）\）。
- 我们说分区\(X\)是微不足道的如果它恰好有一个部分。
- 我们将使用括号表示法，\（[S] _ {x} \），以表示包含\（s \）的\（x \）中的唯一部分。所以这就像给定元素的等价类。
- 然后我们将使用符号\（s〜{x} t \）来说，两个元素\（s \）和\（t \）在同一部分中\（x \）。
您也可以将分区视为与set \（s \）上的变量相同。以这种方式观看，分区\（x \）的值对应于元素所在的部分。
或者你可以想到\（x \）作为一个问题您可以询问有关泛型元素的\(S\)。如果我有一个\(S\)元素，它对你是隐藏的，你想问一个关于它的问题，每个可能的问题对应一个分区，根据不同的可能的答案分割\(S\)。
我们还会用到格子结构分区：
- We’ll say that \(X \geq_S Y\) (\(X\) is finer than \(Y\), and \(Y\) is coarser than \(X\)) if \(X\) makes all of the distinctions that \(Y\) makes (and possibly some more distinctions), i.e., if for all \(s,t \in S\), \(s \sim_X t\) implies \(s \sim_Y t\). You can break your set \(S\) into parts, \(Y\), and then break it into smaller parts, \(X\).
- \（x \ vee_s y \）（\（x \）和\（y \）的常见细化是比\（x \）和\（y \）更精细的粗糙分区。这是唯一的分区，它使得\（x \）或\（y \）所做的所有区别，而且没有其他区别。这是明确的，我不会在这里展示。
希望这主要是背景。现在我想展示一些新的东西。
(第一部分，主体)···设置accipizations.
一种分解集合中的\(S\)是由\(S\)的非平凡分区组成的集\(B\)，称为因素，使每一种从\(B\)中的每个因子中选择一个部件的方法，在这些部件的交点中存在唯一的\(S\)元素。
所以这可能有点密集。我的简短标记线是：“\（s \）的分解是一种观看\（s \）作为产品的方法，以与分区是一种观看\（s \）作为一个方法不相交联盟。“
如果您从第一次谈话中拍摄了一个定义，则应该是分解的定义。我会尝试从一堆不同的角度解释它来帮助传达这个概念。
if \（b = {b_0，\ dots，b_ {n} \} \）是\（s \）的分解，那么存在\（s \）和\（b_0 \ times \ dots \之间的两突发\（s \ mapsto（[s] _ {b_0}，\ dots，[s] _ {b_ {n}}）给出的次数b_ {n}）。该双射将从\（s \）的元素发送到只有包含该元素的部件组成的元组。并且由于这种自由度，\（| s | = \ prod_ {b \ in b} | b | \）。
因此，我们真的将\（s \）视为这些个体因素的产品，没有额外的结构。
虽然我们不会在这里证明这一点，但您可以验证的其他东西是一个因子中的所有部分都必须具有相同的大小。
我们将写\(\mathrm{Fact}(S)\)用于\(S)的所有因子分解的集合，我们将说a有限的因素集是一对\（（s，b）\），其中\（s \）是一个有限集和\（b \ in \ mathrm {suf} \）。
请注意，\（s \）和\（b \）之间的关系有点循环。如果我想定义一组因子，我可以使用两种策略。我可以首先介绍\（s \），并将其分为因素。或者，我可以首先介绍\（b \）。任何我有一个有限集合的有限集合\（b \），我可以拿起他们的产品，从而产生一个\（s \），modulo的一些集合是空的。所以\（s \）只能成为一个有限的任意有限组集合的产品。
对我的眼睛来说，这种因素的概念非常自然。它基本上是集分区的乘法模拟。我真的想推动那一点，所以这是另一种推动这一点的尝试：
| 一种划分是一个设置\（x \）非空 子集\（s \）这样明显的 功能从这脱节联合的 \（x \）的元素至\（s \）是一个自杀。 |
一种分解的集合是什么非琐碎 分区\（s \）这样明显的 功能至这产品的 \(B\)的元素从\（s \）是一个自杀。 |
我可以从之前的分区定义进行略微修改的版本，并在一系列单词中进行两种单词，并取出设置的分解定义。
希望你现在有点相信这是一个非常自然的概念。
| 安德鲁·克克：斯科特在一个意义上，您将“子集”视为双重分区，我认为是有效的。然后在另一个意义上，你将“分解”视为双重分区。那些都有效，但也许值得谈论两种二元性。 斯科特：是的。我认为有什么样的方法可以查看分区。您可以将分区视为“双向子集的分区”，并且您也可以将分区视为从子集中建立的内容。这两个不同的观点在双重化时会做出不同的事情。 拉库马:我正要去检查:你说你可以从一个任意的\(B\)开始，然后从它构建\(S\)。它可以是任意的集合，然后总是有一个\(S\)… 斯科特：如果没有一个是空的，是的，你可以取任意元素集合的集合。你可以取它们的乘积，你可以用一个集合中的每一个元素来确定投影到那个元素上的乘积的子集。 拉库马:啊。所以\（s \）在那种情况下只会是元组。 斯科特：这是正确的。 布伦丹奉：斯科特，给定了一套，我发现很容易提出分区。但我发现患者难以容易提出。你有什么技巧吗？ 斯科特：对于这个，我应该继续举例子。 Joseph Hirsh：在你这样做之前，我可以问一件事吗？您允许因素在其中有一个元素吗？ 斯科特：我说“不动性”，这意味着它没有一个元素。 Joseph Hirsh：“非动力”意味着“没有一个元素，而不是没有元素”？ 斯科特：不，空集有分区（没有零件），我会称之为不动的。但空套的东西并非如此至关重要。 |
我现在要继续一些例子。
(第一部分，例子)····枚举因素
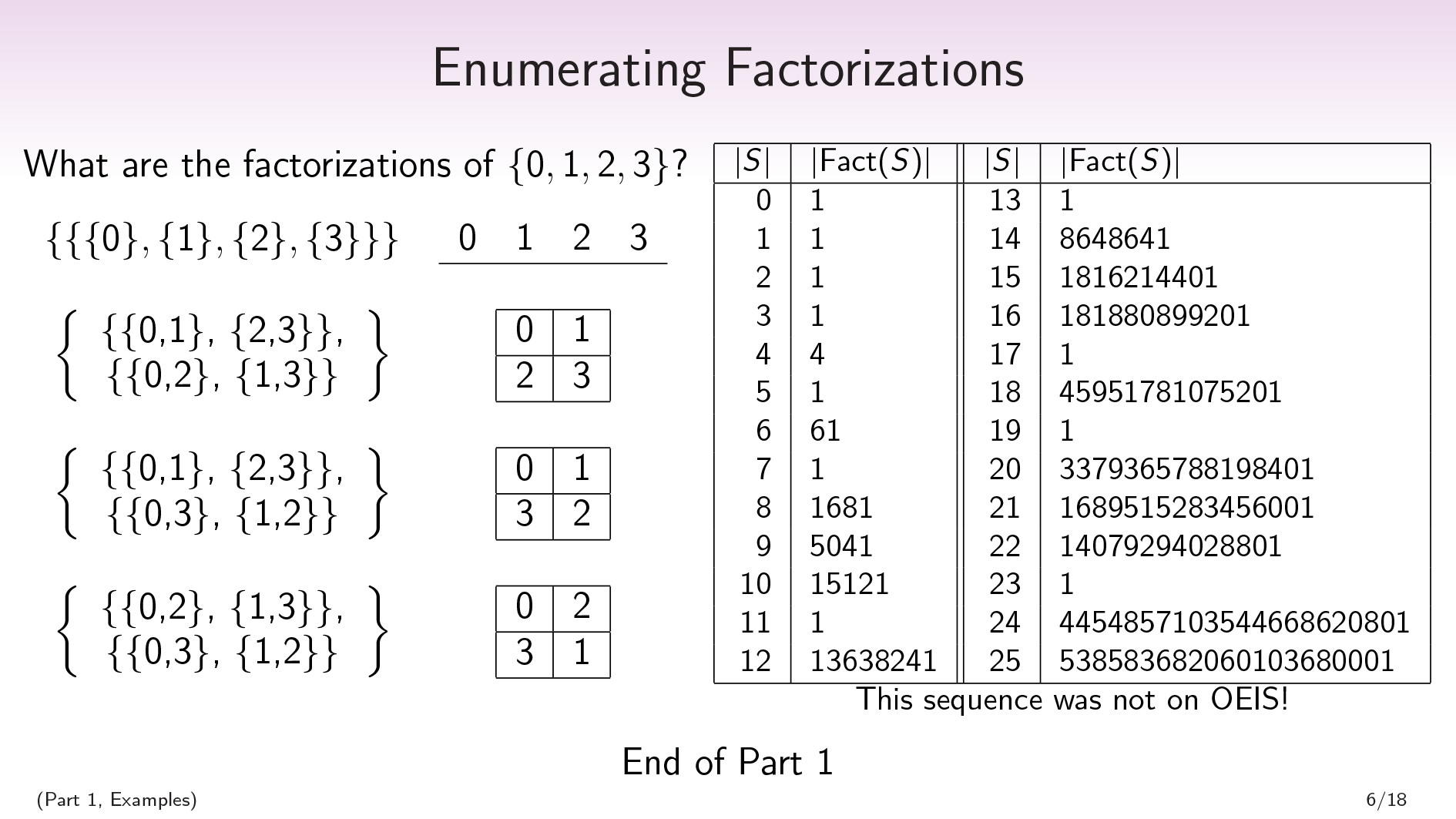
锻炼!集合\(\{0,1,2,3\}\)的因数是什么?
扰流器空间：
．
．
．
．
．
．
．
．
．
．
．
．
．
．
首先，我们要做一个平凡的因式分解
\（\ begin {split} \ {\ \ {\ {\ {\ {0 \}，\ {1 \}，\ {2 \}，\ {3 \} \} \ \ \} \ END {split} \ begin {拆分} \ \ \ \ {\ 0 \ \ \ 1 \ \ \ \ 2 \ \ \ 3 \} \ END {split} \）
我们只有一个因子，这个因子就是离散分割。你可以对任何集合这样做，只要你的集合至少有两个元素。
回想一下，在分解的定义中，我们希望为从每个因素选择一个部分的方式，我们在这些部分的交叉点中有一个唯一的元素。由于我们这里只有一个因素，满足定义只需要从离散分区选择一个部分，因此存在于该部分中的唯一元素。
然后我们想要一些较少的琐碎的因素。为了有一个分解，我们将需要一些分区。我们分区的基数的产物将不得不等于我们集合的基数，即4。
表达4作为非活动产品的唯一方法是将其表达为\（2 \ times 2 \）。因此，我们正在寻找具有2个因素的因素，每个因素都有2个部分。
我们之前注意到，一个因子中的所有部件必须是相同的尺寸。我们要找两个分区每个分区都能把4个元素的集合分成2个大小为2的集合。
So if I’m going to have a factorization of \(\{0,1,2,3\}\) that isn’t this trivial one, I’m going to have to pick 2 partitions of my 4-element set that each break the set into 2 parts of size 2. And there are 3 partitions of a 4-element sets that break it up into 2 parts of size 2. For each way of choosing a pair of these 3 partitions, I’m going to get a factorization.
\（\ begin {split} \ begin {bmatrix} \ \ \ \ {\ {0,1 \}，\ {2,3 \} \}，\ \\ \ {\ {0,2 \}，\ {1那3.\}\} \end{Bmatrix} \end{split} \begin{split} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \begin{array} { |c|c|c|c| } \hline 0 & 1 \\ \hline 2 & 3 \\ \hline \end{array} \end{split}\)
\（\ begin {split} \ begin {bmatrix} \ \ \ \ \ {\ {0,1 \}，\ {2,3 \} \}，\ \\ \ {\ {0,3 \}，\ {1那2\}\} \end{Bmatrix} \end{split} \begin{split} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \begin{array} { |c|c|c|c| } \hline 0 & 1 \\ \hline 3 & 2 \\ \hline \end{array} \end{split}\)
\（\ begin {split} \ begin {bmatrix} \ \ \ \ {\ {0,2 \}，\ {1,3 \} \}，\ \\ \ {\ {0,3 \}，\ {1那2\}\} \end{Bmatrix} \end{split} \begin{split} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \begin{array} { |c|c|c|c| } \hline 0 & 2 \\ \hline 3 & 1 \\ \hline \end{array} \end{split}\)
所以4个元素的集合有4个因式。
一般来说，你可以问，“有多少尺寸尺寸\（n \）？”。这是一个小图表，显示\（n \ LEQ 25 \）的答案：
| \ (| | \) | \（| \ mathrm {事实}（s）| \） |
| 0. | 1 |
| 1 | 1 |
| 2 | 1 |
| 3. | 1 |
| 4. | 4. |
| 5. | 1 |
| 6. | 61 |
| 7. | 1 |
| 8. | 1681 |
| 9. | 5041. |
| 10. | 15121. |
| 11. | 1 |
| 12. | 13638241 |
| 13. | 1 |
| 14. | 8648641 |
| 15. | 1816214401. |
| 16. | 181880899201. |
| 17. | 1 |
| 18. | 45951781075201 |
| 19. | 1 |
| 20. | 3379365788198401 |
| 21. | 1689515283456001 |
| 22. | 14079294028801 |
| 23. | 1 |
| 24. | 4454857103544668620801 |
| 25. | 538583682060103680001. |
你会注意到，如果\（n \）是素数，则会有一个单一的分解，希望有意义。这是只有一个因素的分解。
一个让我非常惊讶的事实是这个序列没有出现oeis.这个数据库是组合学家用来检查他们的序列之前是否被研究过，以及看看与其他序列的联系。
对我来说，这感觉就像乘法版本贝尔的数字．贝尔号码计算有一组大小的分区数量\（n \）。这是OEIS的序列号110，超过300,000;即使我调整它并删除退化案例，此序列也没有显示出来并删除退化案例。
我对这个事实非常困惑。对我来说，沉思似乎是一个极其自然的概念，在我看来看起来并没有真正研究过。
这是我的短组合谈话的结束。
| 拉库马:如果您愿意这样做，我会感谢刚刚介绍要素和定义的一个例子，因为这对我来说很新。 斯科特：是的。让我们经历第一个非\（\ {0,1,2,3 \} \）的非活动分解： \（\ begin {split} \ begin {bmatrix} \ \ \ \ {\ {0,1 \}，\ {2,3 \} \}，\ \\ \ {\ {0,2 \}，\ {1那3.\}\} \end{Bmatrix} \end{split} \begin{split} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \begin{array} { |c|c|c|c| } \hline 0 & 1 \\ \hline 2 & 3 \\ \hline \end{array} \end{split}\) 在定义中，我说过一个因式分解应该是一组分区这样每一种从每个分区中选择一个部分的方法，在这些部分的交点中会有一个唯一的元素。 在这里，我有一个分隔小数字和大数字的分区:\(\{\{0,1\}，\{2,3\}\)。我还有一个分隔偶数和奇数的分区:\(\{\{0,2\}，\{1,3\}\)。 目的是，对于选择“小”或“大”而且选择“偶数”或“奇数”，将有一个唯一的元素，这是这两个选择的结合。 在另外两个非活动的因素中，我用“内部和外部”区别替换为“小而大”或“偶数和奇数”。 David Spivak：对于分区和许多事情，如果我知道集合\（a \）的分区和set \（b \）的分区，那么我知道一些\（a + b \）的分区（不相交的union）或者我知道一些\（a \ times b \）的分区。您是否知道要素的任何事实？ 斯科特：是的。如果我有两个事务集，我可以获得一系列因素，他们的产品，哪种不相交的一系列因素。对于添加剂的东西，你不会得到这样的东西，因为Prime Set没有任何非凡的因素。 |
好吧。我想我要进入主题了。
（第2部分，标题幻灯片）···主谈（这是关于时间）
（第2部分，动机）···珍珠范式
没有谈论，我们无法谈论时间珍珠因果推断．首先我想说的是，我认为Pearlian的范例是伟大的。这给了我一些疯狂的观点，但我要说，这是自爱因斯坦以来我们对时间的理解中发生的最好的事情。
我不会在这里进入珍珠范例的所有细节。我的谈话在技术上不会依赖它;它在这里是为了动力。
给定变量集合和这些变量的联合概率分布，Pearl可以推断变量之间的因果/时间关系。(在这次谈话中，我将交替使用“因果”和“时间”，尽管从哲学角度来说，这里可能有更有趣的事情要说。)
珍珠可以从统计数据推断时间数据，这是违背“相关性并不意味着因果关系”的格言。这就像珍珠正在采取相关性的组合结构，并使用它来推断出来，我认为这真的很棒。
| 拉库马:我可能错了，但我认为这是假的。或者我认为这并非所有珍珠需求 - 只是对变量的联合分布。他还没有使用干预分布吗？ 斯科特：在本书中第二章中描述的理论中因果关系，他并不真正使用其他东西。珍珠在其他地方建立了这种更大的理论。但是你有一些强有力的能力，也许假设简单或任何（但不是假设您可以访问额外信息），以获取变量的集合和这些变量的联合分布，并从相关性推断出来。 安德鲁·克克：Ramana，它取决于潜在因果图的结构。对于一些因果图，您实际上可以唯一的恢复，没有干预措施。只需要具有零测量异常的假设，这真的很强大。 拉库马:对，但随后您使用的信息是图形。 安德鲁·克克：不,你不是。就是联合分布。 拉库马:哦好的。对不起，继续前进。 安德鲁·克克：这re exist causal graphs with the property that if nature is generated by that graph and you don’t know it, and then you look at the joint distribution, you will infer with probability 1 that nature was generated by that graph, without having done any interventions. 拉库马:明白了。这是有意义的。谢谢。 斯科特：凉爽的。 |
不过，我打算(稍微)反对这一点。我要去认领珍珠是在制作此推断时的作弊。我要指出的是，在句子中，在“给定变量的集合和这些变量上的联合概率分布，珍珠可以推断变量之间的因果/时间关系。”，给定集变量之间的单词是实际上隐藏了很多工作。
强调通常符合联合概率分布，但珍珠不是单独从统计数据推断出时间数据。他从统计数据推断出时间数据和分解的数据：世界如何分解为这些变量。
我认为这个问题还与未能充分处理抽象和决定论有关。为了说明这一点，我们可以这样说:
“好吧，如果我拍摄了珍珠问题的变量，我怎么办我只是忘记那个结构？我可以拍摄我给出的所有这些变量的产物，并考虑我所赋予的变量产品的所有分区的空间;每个分区中的每个分区都将是自己的变量。然后我可以尝试在这大珠子的因果推断下，我通过忘记给我的变量的结构而得到的所有变量。“
问题是，当你这样做时，你有一堆是彼此的确定性函数的东西，你实际上无法使用珍珠范式推断。
所以在我看来，这种作弊非常纠缠在于珍珠的范式对处理抽象和决定论并不擅长。
（第2部分，目录）···我们可以做得更好
我们将在这次谈话中做的主要事情是我们将介绍一个不依赖于分解数据的珍珠的替代品，因此随着抽象和决定论更好地工作。
如果珍珠被赋予了一系列变量，我们将考虑给定集的所有分区。珍珠揭开了一条定向的无循环图，我们将推断有限的成分集。
在Pearlian的世界里，我们可以从图表中读出时间和正交/独立的性质。节点之间的有向路径对应于一个节点在另一个节点之前，如果两个节点没有共同的祖先，则它们是独立的。类似地，在我们的世界里，我们可以从一个有限因式集合中读出时间和正交性。
（正交和独立性都很相似。当我谈论一个组合概念时，我会使用“正交性”这个词，当我谈论概率概念时，我会使用“独立”。）
在珍珠世界，D.-分离，你可以从图上读出来，它对应于所有概率分布的条件独立性，你可以把它放到图上。我们将得到一个基本定理它基本上说的是同样的事情条件正交对应于条件独立性在所有的概率分布中我们可以放到因式集合中。
在珍珠世界，D.-分离将满足组合书写体公理。在我们的世界里，我们只需要满足组合半图公理。第五个graphoid公理是一个你从一开始就不应该想要的。
珍珠会出现因果推断。我们将讨论如何使用这种新的范例进行时间推断，并推断出一些非常基本的时间事实，即珍珠的方法不能。（请注意，珍珠也有时会推断出颞关系我们无法 - 但仅从我们的角度来看，因为珍珠正在进行额外的分解假设。）
然后我们将讨论一堆应用程序。
| 珍珠 | 这个谈话 |
| 给定的变量集合 | 给定集合的所有分块 |
| 有向无环图 | 有限的因素集 |
| 节点间有向路径 | “时间” |
| 没有共同的祖先 | “正交性” |
| D.- | “有条件的正交性” |
| 组成石灰 | 成分Semigraphoid |
| D.- 分子↔有条件独立性 | 基本的定理 |
| 因果推论 | 时间推断 |
| 许多应用程序 | 许多应用程序 |
除了动机，目录和示例部分中，该表也可以作为两个会谈的轮廓。我们已经讨论了设置分区和有限因子集，所以现在我们将谈论时间和正交性。
（第2部分，主体）···时间和正交性
我认为如果从谈话的第二部分捕获一个定义，那应该是这个。鉴于一个有限的因素集作为上下文，我们将定义分区的历史记录。
让\（f =（s，b）\）是一个有限的成分集。并且让\（x，y \ in \ mathrm {part}（s）\）是\（s \）的分区。
这历史for all \(s, t\ in s \)， if \(s \sim_b t) for all \(B\ in h \)，则\(s \sim_X t)。
\ (X \)的历史,然后,是最小的一组因素\ (H \)所以,\ B \)——的最小子集,如果我把一个元素\(\)我从你隐藏它,你想知道哪一部分\ (X \)在,只要我告诉你它是哪一部分的每个因素\ (H \)。
因此，历史\（h \）是一组\（s \）的因素，并且了解\（h \）中所有因素的值足以知道\（x \）的值，或者知道which part in \(X\) a given element is going to be in. I’ll give an example soon that will maybe make this a little more clear.
然后我们来定义时间从历史。我们说\(X\)是弱之前写\ \ (Y \) (X \ leq ^ Y F \),如果\ (h ^ F (X) \ subseteq h ^ F (Y) \)。我们说\(X\)是严格的前\（y \），写入\（x <^ f y \），if \（h ^ f（x）\ subset h ^ f（y）\）。
一个类比可以绘制的是这些历史就像时空的点的过去光锥。当一个点在另一点之前时，那么较早点的向后光锥将是后来点的向后锥体的子集。这有助于显示为什么“之前”可以像一个子集关系。
我们也将从历史上定义正交性。我们会说两个分区\（x \）和\（y \）是正交写\ (X \补^ \)财政年度,如果他们的历史是不相交的:\ (h ^ F (X) \帽h ^ F (Y) = \{\} \)。
现在我要经历一个例子。
（第2部分，实施例）···生命的游戏
设\(S\)是所有生命游戏计算的集合，从一个\([-n,n]\次[-n,n]\)板开始。
让\ (R = \ {(R、c、t) \ \ mathbb {Z} ^ 3 \ mid0 \ leq t \ leq n, \ \) \ (R | | \ leq次方,c | \ \ | leq次方\}\)(例如,细胞可以计算从最初\ ((- n, n) (- n, n) \ \倍)董事会成员)。对于r\)中的\((r,c,t)\，让\(\ell(r,c,t)\subseteq S)是所有计算的集合，使行\(r)和列\(c)的单元格在r\ (t)时是活的。
（Minor footnote: I’ve done some small tricks here in order to deal with the fact that the Game of Life is normally played on an infinite board. We want to deal with the finite case, and we don’t want to worry about boundary conditions, so we’re only going to look at the cells that are uniquely determined by the initial board. This means that the board will shrink over time, but this won’t matter for our example.)
\（s \）是所有生活游戏的集合，但由于生命游戏是确定性的，所以所有计算的集合都与所有初始条件的集合相对应。所以\（| s | = 2 ^ {（2n + 1）^ {2}} \），初始板状态的数量。
这也为我们提供了对所有生命游戏集合的一个很好的分解。For each cell, there’s a partition that separates out the Game of Life computations in which that cell is alive at time 0 from the ones where it’s dead at time 0. Our factorization, then, will be a set of \((2n+1)^{2}\) binary factors, one for each question of “Was this cell alive or dead at time 0?”.
正式：对于\（（r，c，t）\在r \）中，让\（l _ {（r，c，t）} = \ {\ ell（r，c，t），s \ setminus \ ell（r，c，t）\} \）。设\（f =（s，b）\），其中\（b = \ {l _ {（r，c，0）} \ mid-n \ leq r，c \ leq n \} \）。
这套我们可以谈论的所有生命计算的所有游戏中也会有其他分区。例如，您可以采取单元格和时间\（t \）并说：“此单元格在时间\（t \）？”，并且将有一个分区，将该单元格固定的计算分开at time \(t\) from the computations where it’s dead at time \(t\).
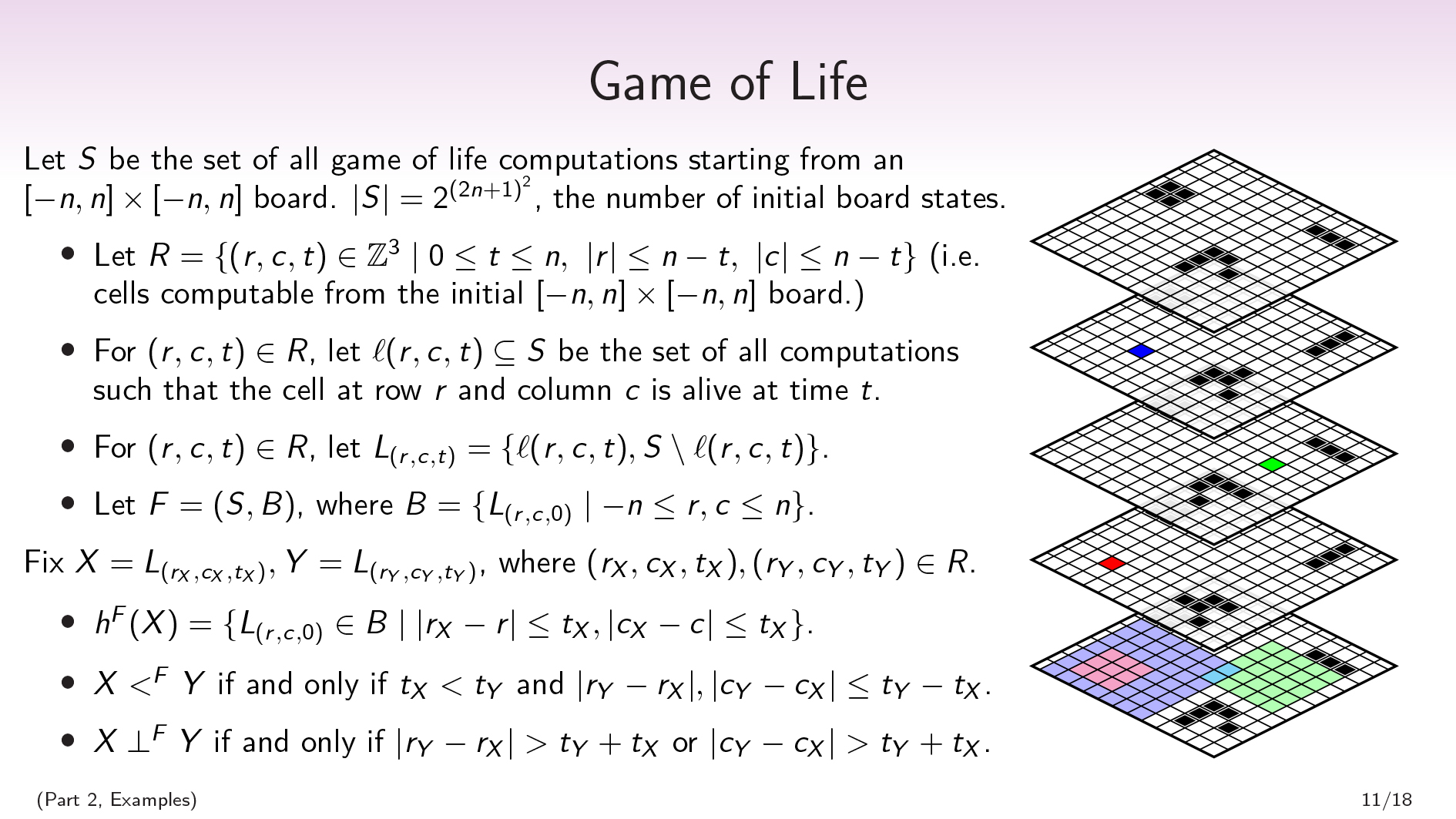
这里有一个例子:
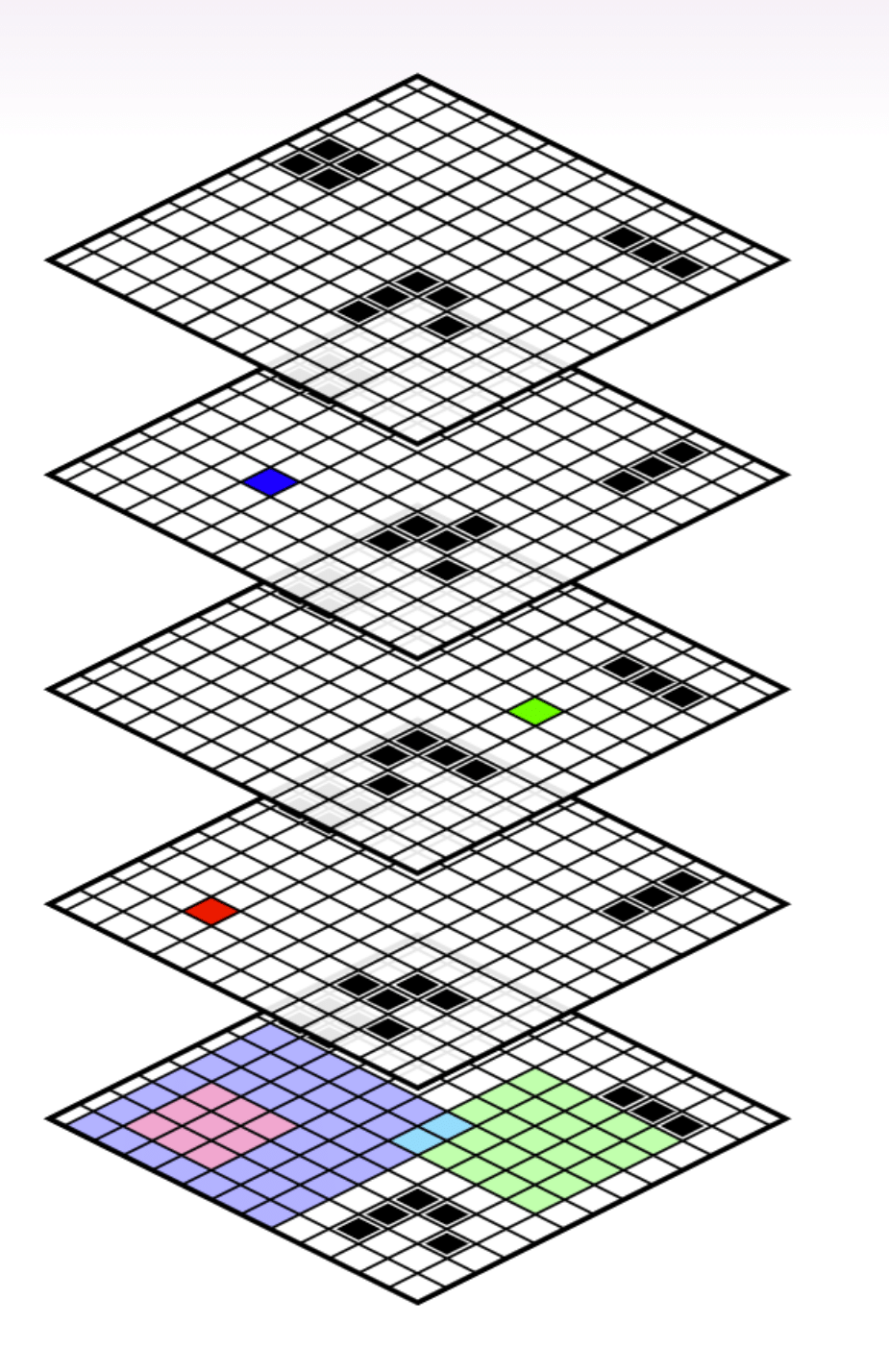
最低的网格显示初始板状态的一部分。
上板上的蓝色，绿色和红色方块是（细胞，时间）对。每个方块都对应于所有生命游戏集合的分区，“在给定的时间\（t \）存在或死亡是\（t \）？”
该分区的历史将是初始板中的所有单元格，用于计算细胞是否在时间\（t \）中是否存在。这就是概念弄清楚细胞的状态。例如，知道初始板中的九个光线的状态始终告诉您第二板中的红细胞的状态。
在该示例中，对应于红小区状态的分区是严格地在与蓝单元对应的分区之前。红色细胞是否活着或死亡的问题是在蓝色细胞活着或死亡的问题之前。
同时，红细胞是否活着或死亡的问题将是正交对于绿色细胞是否活着或死亡的问题。
和蓝色细胞是否活着或死亡的问题是不与绿色细胞是活着还是死的问题，因为它们与青色细胞相交。
概括点，修复\（x = l _ {（r_x，c_x，t_x）}，y = l _ {（r_y，c_y，t_y）} \），其中\（（r_x，c_x，t_x），（r_y，c_y，t_y）\在r \）。然后：
- \（h ^ {f}（x）= \ {l _ {（r，c，0）} \ in b \ mid | \ leq t_x，| c_x-c | \ leq t_x \} \）。
- \（x \ᐸ^ {f} \ y \）如果才可\（t_x \ᐸ\ t_y \）和\（| r_y-r_x |，| c_y-c_x | \ LEQ T_Y-T_X）。
- \ (X \ F补^ Y \)当且仅当\ (| r_Y-r_X | > t_Y + t_X \)或\ (| c_Y-c_X | > t_Y + t_X \)。
我们还可以看到蓝色和绿色细胞的样子几乎正交。如果我们在历史交叉口中的两个青色细胞的值，然后蓝色和绿色分区变得正交。这就是我们接下来要讨论的事情。
| David Spivak：根据先验，那将是一个巨大的计算——能够告诉我你理解生命游戏的因式分解结构。那么你是用什么直觉来得出这个结论的呢，它有你暗示的这种因式分解结构? 斯科特：所以，我已经定义了分解结构。 David Spivak：你已经给了我们一个因数分解。所以你会有一个很好的直觉历史， 我猜。也许这就是我询问的。 斯科特：是的。所以，如果我没有给你分解，那么你可以在这里放在这里的这种讨厌的因素数量。然后对于历史，我正在使用的直觉是：“我需要知道什么，以计算这个值？” 我实际上经历了，我在生活中的游戏中取得了很少的小工具，以确保我在这里，每个单个细胞实际上都可以在某些情况下影响有问题的细胞。但是，是的，我正在努力的直觉主要是关于计算中的信息。它是“我可以建立一个情况，如果我知道这个事实，我就能计算这个值是什么？如果我不能，那么它可以采取两个不同的值。“ David Spivak：好吧。我想从定义中推导出这种直觉是我所遗漏的，但我不知道我们是否有时间来完成它。 斯科特：是的，我想我不会去这里。 |
（第2部分，主体）···有条件的正交性
所以，让我们设定一下预期:每次我向别人解释皮尔因果推理时，他们都会这么说D.- 他们不记得的事情。D.- 比珍珠中珍珠中的“没有任何共同祖先”和“没有任何共同祖先之间的指向的路径更复杂的概念;同样，条件正交性比我们范例中的时间和正交性更复杂。虽然我确实认为有条件的正交性具有比较简单更简单的定义D.- 酸化。
我们将从条件历史的定义开始。我们同样有一个固定的有限集合作为环境。设\(F=(S,B))是一个有限因子集，设\(X,Y,Z in\text{Part}(S))，设\(E\subseteq S)。
已知\(E\)的\(X\)条件历史，写成\(h^F(X|E)\)，是满足以下两个条件的最小因子\(h \subseteq B)的集合:
- 对于所有\（s，t \在e \）中，如果\（s \ sim_ {b} t \）所有\（b \ in h \），那么\（s \ sim_x t \）。
- 对于所有\（s，t \中的e \）和\（r \在s \中），如果\（r \ sim_ {b_0} s \）所有\（b_0 \在h \）和\（r \ sim_{b_1} t \）对于所有\（b_1 \在b \ setminus h \）中，然后\（r \在e \中）。
第一个条件很像我们在历史定义中的条件，除了我们要假设我们在\(E\)中。所以第一个条件是:如果你只知道一个对象在\(E\)中，你想知道它在\(X\)中的哪个部分，它足以让我告诉你它在历史\(H\)中的每个因子中的哪个部分。
我们的第二个条件实际上并没有提及\（x \）。这将是\（e \）和\（h \）之间的关系。它说，如果要弄清楚\（s \）的元素是否处于\（e \），则足以并行化并提出两个问题：
- “如果我只查看\（h \）中的因素的值，就是'这一点是\（e \）'与该信息兼容？”
- “如果我只看看\（b \ setminus h \）中的因素的值，那么'这一点是\（e \）'与该信息兼容吗？”
如果这两个问题都返回“是”，那么点必须处于\（e \）。
我不会给出一个直观的解释为什么这需要成为定义的一部分。我要说的是，如果没有第二个条件，条件历史甚至无法定义，因为它在交点下不会闭合。所以我不能在子集排序中取最小的因子集合。
我不是通过解释它背后的直觉来证明这个定义，而是通过使用它并诉诸于它的结果来证明它。
我们将使用条件历史来定义条件正交性，就像我们使用历史来定义正交性。我们说\（x \）和\（y \）是正交给定\（e \ subseteq s \），写入\（x \ perp ^ {f} y \ mid e \），如果给定的\（x \）历史记录\（e \）与\（y的历史记录是不相交的给定\（e \）：\（h ^ f（x | x | e）\ cap h ^ f（y | e）= \ {\} \）。
我们说\（x \）和\（y \）是正交给定\（z \ in \ text {part}（s）\），写入\（x \ perp ^ {f} y \ mid z \），if \（x \ perp ^ {f} y \ mid z \）for所有\（z \ z \）。所以在给定分区的情况下，它意味着正交的是什么，鉴于分区可能是分区的每个单独的方式，每个单独的方式都是正交。
我已经做了一段时间了，我觉得这很自然，但我没有一个好的方法来推动这种情况的自然。所以，我还是想诉诸于结果。
（第2部分，主体）···组成半映射公理
有条件的正交性满足成分semigraphoid公理，这意味着有限的成分集是相当良好的。
设\(F=(S,B)\)是一个有限因子集，设\(X,Y,Z,W)在\text{Part}(S)\)中是\(S)的分区。然后：
- 如果\（x \ perp ^ {f} y \ mid z \），那么\（y \ perp ^ {f} x \ mid z \）。（对称）
- 如果\ (X \补^ {F} Z中期(Y \ vee_S W) \ \),然后\ (X \补^ {F} Y中期\ Z \)和\ (X \补^ {F} W \ Z中期\)。（分解）
- 如果\（x \ perp ^ {f}（y \ vee_s w）\ mid z \），那么\（x \ perp ^ {f} y \ mid（z \ vee_s w）\）。（弱联盟）
- 如果\（x \ perp ^ {f} y \ mid z \）和\（x \ perp ^ {f} w \ mid（z \ vee_s y）\），那么\（x \ perp ^ {f}（y\ vee_s w）\ mid z \）。（收缩）
- 如果\（x \ perp ^ {f} y \ mid z \），如果\（x \ perp ^ {f} w \ mid z \），那么\（x \ perp ^ {f}（y \ vee_s w）\ mid z \）。（作品）
此处的前四个属性构成了半映射公理，略微修改，因为我正在使用分区而不是变量集，所以联盟被常用的细化替换。还有另一个石灰石公理，我们不会满足;但我认为我们不想满足它，因为它与决定论没有很好。
这里的第五财产是，组成，也许是最不行性的，因为它并不完全满足概率的独立性。
分解和组成是彼此的相互关系。在整个\（z \）上的调节，他们说\（x \）与\（y \）和\（w \）正交，如果\（x \）与常用改进\（x \）是正交的\（y \）和\（w \）。
（第2部分，主体）···基本的定理
除了表现良好，我还想表明条件正交性很强大。我想要做到这一点的方式是通过显示条件正交性完全对应于您可以放在有限因子集中的所有概率分布中的条件独立性。因此，很像D.- 在珍珠图片中，有条件正交性可以被认为是概率独立的组合形象。
一种有限因子集的概率分布\(F=(S,B)\)是\(S)上的一个概率分布\(P)可以被认为是来自于\(B)中每个因子上的一组独立的概率分布。所以\ (P (s) = \ prod_ {b \ b} P ([s] _b) \)为所有\ \ s \)。
这种有效意味着您的概率分布因子与您的设定因子相同：任何给定元素的概率是它在每个因素内的每个各个部件的概率的乘积。
这有限因子集的基本定理说：让\（f =（s，b）\）是一个有限的因子集，让\（x，y，z \ in \ text {part} \）是\（s \）的分区。然后\（x \ perp ^ {f} y \ mid z \）如果且仅在\（f \）上的所有概率分布\（p \），并且所有\（x \中），\（y\在y \）中，\（z \在z \中），我们有\（p（x \ cap z）\ cdot p（y \ cap z）= p（x \ cap y \ cap z）\ cdot p（z）\）。即，\（x \）与\（z \）of \（z \）在所有概率分布中满足时\（z \）。
对我来说，这个定理有点不可能证明。我不得不通过定义与子集相关的某些多项式，然后在这些多项式的空间中处理独特的分解;我认为证据是八页或其他东西。
基本定理允许我们从概率数据中推断出正交数据。如果我有一些经验分布，或者我有一些贝叶斯分布，我可以使用它来推断一些正交性数据。（我们还可以想象来自其他来源的正交性数据。）然后我们可以使用这种正交性数据来获得时间数据。
所以接下来，我们将讨论如何从正交数据获取时间数据。
（第2部分，主体）···时间推断
我们从一个有限集合开始，也就是我们的样本空间。
你可能认为我们会尝试做的一件幼稚的事情是推断出\(\Omega\)的因数分解。我们不会这么做，因为这样限制太大了。我们想让\(\Omega\)可能对我们隐藏一些信息，因为有一些潜在的结构等。
可能存在一些情况下明确而不是在\（\ omega \）中没有明显。So instead, we’re going to infer a factored set model of \(\Omega\): some other set \(S\), and a factorization of \(S\), and a function from \(S\) to \(\Omega\).
\（\ omega \）模型是一对\（（f，f）\），其中\（f =（f =（f =（s，b）\）是一个有限的因子集和\（f：s \ lightarrow \ omega \）。（\（f \）不需要是注射或形状的。）
然后，如果我有一个\（\ omega \）的分区，我可以在\（f \）后向后向后发送此分区并获得\（s \）的唯一分区。如果\（x \ in \ text {parts}（\ omega）\），则\（f ^ { - 1}（x）\ in \ text {east}（s）\）由\（s \ sim_{f ^ { - 1}（x）} t \ leftrightarrow f（s）\ sim_x f（t）\）。
然后我们要做的是占据一堆关于\（\ omega \）的正交事实，我们将尝试找到一个捕获正交事实的模型。
我们将采取正交数据库在\（\ omega \）上，这是一对\（d =（o，n）\），其中\（o \）（对于“正交”）和\（n \）（for“not正交”）是\（\ omega \）分区的每组三级\（（x，y，z）\）。我们将认为这些是关于正交性的规则。
它意味着模型\（（f，f）\）来满足数据库\（d \）是：
- \（f ^ { - 1}（x）\ perp ^ {f} f ^ { - 1}（y）\ mid f ^ { - 1}（z）\）只要\（（x，y，z）\在o \），和
- \（\）\（\ lnot（f ^ { - 1}（x）\ perp ^ {f} f ^ { - 1}（y）\ mid f ^ { - 1}（z））\）每当\（（x，y，z）\在n \中。
我们要满足这些正交性规则，我们要考虑所有符合这些规则的模型的空间。虽然总是会有无穷多模型与数据库一致,如果至少有一个是你可以随时添加更多信息,然后删除\ (f \)——我们希望有时能推断出所有满足我们的数据库模型,\ (f ^ {1} (X) \) \之前(f ^ {1} (Y) \)。
这就是我们推断时间的意思。如果所有与数据库(D)一致的模型(F, F)都满足一些关于时间的要求(F ^{-1}(X) \ᐸ^F F ^{-1}(Y)\)，我们将说(X \ᐸ_D \ Y)。
（第2部分，实施例）···两个二进制变量（珍珠）
所以我们已经建立了这种漂亮的组合概念的时间推断。明显的下一个问题是：
- 我们是否可以使用这种方法推断有趣的事实，或者是空虚的吗？
- 和：这个框架如何与珠子时间推断进行比较？
珍珠时间推理真的很强大;鉴于足够的数据，它可以在各种情况下推断时间序列。有限因子集比较有多强大？
为了解决这个问题，我们将去一个例子。让（x \）和\（y \）是两个二进制变量。珍珠问：“是\（x \）和\（y \）独立？”如果是，则两者之间没有路径。如果否，则可能存在从\（x \）到\（y \）的路径，或从\（y \）到\（x \），或者从第三变量到\（x \）和\（y \）。
无论哪种情况，我们都不能推断出任何时间关系。
对我来说，感觉就是这样的谚语“相关性并不意味着因果关系”来自。珍珠真的需要更多的变量，以便能够从更丰富的组合结构中推断颞关系。
However, I claim that this Pearlian ontology in which you’re handed this collection of variables has blinded us to the obvious next question, which is: is \(X\) independent of \(X \ \mathrm{XOR} \ Y\)?
在Pearlian的世界里，\(X\)和\(Y\)是我们的变量，而\(X\ \mathrm{XOR} \ Y\)只是对这些变量的一些随机操作。在我们的世界中，\(X\ \mathrm{XOR} \ Y\)相反是一个与\(X\)和\(Y\)相同基础上的变量。我对变量\(X\)和\(Y\)做的第一件事是，我取乘积\(X\乘以Y\)，然后我忘记标签\(X\)和\(Y\)。
所以有这个问题，“是\（x \）独立于\（x \ \ mathrm {xor} \ y \）？”如果\（x \）是独立于\（x \ \ mathrm {xor} \ y \），我们实际上将能够得出结论\（x \）是前\（y \）！
So not only is the finite factored set paradigm non-vacuous, and not only is it going to be able to keep up with Pearl and infer things Pearl can’t, but it’s going to be able to infer a temporal relationship from only two variables.
所以让我们经历它的证明。
（第2部分，实施例）···两个二进制变量（因子集）
让（\ omega = \ {0001,10,11 \} \），并让\（x \），\（y \），\（z \）是分区（/ questions）：
- \(x = \{\{00,01\}， \{10,11\}\})。(第一个比特是什么?)
- \ (Y = \{\{00, 10 \} \{01 11 \} \} \)。(第二比特是多少?)
- \（z = \ {00,111 \}，\ {01,10 \} \} \）。（比特匹配吗？）
让\ (D = (O, N) \),在那里\ (O = \ {(X, Z \{\ω\})\}\)和\ (N = \ {(Z, Z, \{\ω\})\}\)。如果我们从概率分布中得到这个正交性数据库，那么我们就不止有两条规则了，因为我们会观察到更多的正交性和非正交性。但是时间推断对于添加更多的规则来说是单调的，所以我们可以使用证明所需的最小规则集。
第一条规则说\(X\)与\(Z\)正交。第二条规则说\(Z\)与自身不正交，也就是说\(Z\)是不确定性的;它说的是\(Z\)中的两个部分都是可能的，都在函数\(f\)下得到支持。\(\{\Omega\}\)表示我们不创建任何条件。
由此，我们将能够证明\（x \ᐸ_d \ y \）。
证明。首先，我们将显示\（x \）之前略微略微\（y \）。让（（f，f）\）满足\（d \）。让\（h_x \）为\（h ^ f（f ^ {-1}（x））\），同样让\（h_y = h ^ f（f ^ { - 1}（y））\）和（h_z = h ^ f（f ^ {-1}（z））\）。
因为\ ((X, Z \{\ω\})O \ \),我们有\ (H_X \帽H_Z = \ {\} \);既然\ ((Z, Z, \{\ω\})\ N \),我们有\ (H_Z \ neq \{\} \)。
因为\（x \ leq _ {\ omega} y \ vee _ {\ oomega} z \） - 因为可以从\（y \）与\（z \） - \（h_x）一起计算\（x \） - \（h_x\ subseteq h_y \ cup h_z \）。（因为分区的历史记录是计算该分区所需的最小因素。）
而且（h_x \ cap h_z = \ {\} \），这意味着\（h_x \ subseteq h_y \），所以\（x \）在\（y \）之前弱。
为了证明严格不等式，我们将假设\(H_X\) = \(H_Y\)。
请注意，可以从\（x \）与\（y \）一起计算\（z \） - 即，\（z \ leq _ {\ oomga} x \ vee _ {\ oomega} y \） - 因此\（H_Z\subseteq H_X\cup H_Y\) (i.e., \(H_Z \subseteq H_X\) ). It follows that \(H_Z = (H_X\cup H_Y)\cap H_Z=H_X\cap H_Z\). But since \(H_Z\) is also disjoint from \(H_X\), this means that \(H_Z = \{\}\), a contradiction.
因此\ (H_X \ neq H_Y \),所以\ H_Y \) (H_X \子集,所以\ (f ^ {1} (X) \ᐸ^ \ f ^ {1} (Y) \),所以\ (X \ᐸ_D Y \ \)。□
当我使用有限的成分集进行时间推断时，我很大程度上都有这样的证据。我们收集了一些关于变量历史的各种布尔组合的空虚或非空虚的事实，并且我们使用这些来得出更多关于彼此的子集的变量历史的更多事实。
我有一个更复杂的例子，它使用条件正交性，而不仅仅是正交性;我不会在这里过来。
我想说的一个有趣的观点是，我们在做时间推断——我们推断\(X\)在\(Y\)之前——但我声明我们也在做概念推断。
想象一下，我有点，它是0或1，它是蓝色或绿色。这两个事实是原始的，独立生成。而且我也有这样的概念，就像“它是grue或bleen？”，这是蓝色/绿色和0/1的\（\ mathrm {xor}）。
有一种感觉，我们推断\（x \）是之前\（y \），并且在这种情况下，我们可以推断出在养殖之前的蓝色。并且这指出了蓝色更加原始的事实，脾气是派生的财产。
在我们的证明中，\(X\)和\(Z\)可以被认为是这些基本属性，而\(Y\)是我们从它们得到的派生属性。所以我们不只是在推断时间;我们在推断什么是好的，自然的概念。我认为这个本体论可以对"你不能真正区分蓝色和蓝色"这句话做些什么就像Pearl对"相关性并不意味着因果关系"这句话所做的一样。
（第2部分，主体）···应用/未来工作/猜测
未来的工作我最兴奋的是有限因子集中化为三个粗略类别：推理（涉及更多计算问题），无限（更多数学）和嵌入式机构（更哲学）。
金宝博娱乐与推论相关的研究主题：
- 暂时推理的可解锁性
- 高效的时间推断
- 概念推断
- 来自原始数据的时间推断和较少的本体假设
- 时间推断具有确定性关系
- 时间不正交性
- 有条件的因素套装
有很多研究方向，比如"我们如何在这个范金宝博娱乐式中进行有效推理"这里的一些问题来自于我们比Pearl做的假设更少的事实，而且在某种意义上更多地来自原始数据。
然后我有关于将因子集扩展到无限案例的应用程序：
- 将定义扩展到无限案例
- 有限维考间集的基本定理
- 连续时间
- 物理学新镜头
我在这次演讲中所展示的一切都是基于有限的假设。在某些情况下，这是不必要的——但在很多情况下，这实际上是必要的，我没有引起注意。
我认为基本定理可以推广到有限维分解集(即，其中\(|b |\)是有限的分解集)，但不能推广到任意维分解集。
然后，我真正兴奋的是嵌入式机构的应用程序：
I focused on the temporal inference aspect of finite factored sets in this talk, because it’s concrete and tangible to be able to say, “Ah, we can do Pearlian temporal inference, only we can sometimes infer more structure and we rely on fewer assumptions.”
但是，我很兴奋的很多应用程序都涉及使用因子集合到模型情况，而不是从数据中推断因子集。
我们目前在任何地方模拟使用图形的图形的情况，即表示信息流或因果关系，我们可能会使用因子来模拟情况;这可能允许我们的模型与抽象更加良好。
我想在建模代理与事物交互时或在建模信息流时建模时，将事故集本体中的替代方案构建。而且我真的很兴奋。
你喜欢这篇文章吗？你可以享受我们的其他分析帖子，包括：
