An agent which is larger than its environment can:
- Hold an exact model of the environment in its head.
- Think through theconsequences每个潜在的行动方案。
- 如果它不完全了解环境,请保持everypossible方式the environment could be in its head, as is the case with Bayesian uncertainty.
All of these are typical of notions of rational agency.
Anembedded agentcan’t do any of those things, at least not in any straightforward way.

One difficulty is that, since the agent is part of the environment, modeling the environment in every detail would require the agent to model itself in every detail, which would require the agent’s self-model to be as “big” as the whole agent. An agent can’t fit inside its own head.
缺乏清晰的代理/环境边界迫使我们努力应对自我参考的悖论。好像代表世界其他地方还不够艰难。
嵌入式世界模型have to represent the world in a way more appropriate for embedded agents. Problems in this cluster include:
- the “realizability” / “grain of truth” problem: the real world isn’t in the agent’s hypothesis space
- logical uncertainty
- high-level models
- 多层模型
- ontological crises
- naturalized induction, the problem that the agent must incorporate its model of itself into its world-model
- anthropic reasoning, the problem of reasoning with how many copies of yourself exist
In a Bayesian setting, where an agent’s uncertainty is quantified by a probability distribution over possible worlds, a common assumption is “realizability”: the true underlying environment which is generating the observations is assumed to have at leastsomeprobability in the prior.
在游戏理论中,通过说先前的“真理”来描述相同的属性。但是,应该指出的是,在游戏理论环境中获得该属性还有其他障碍。因此,在他们常见的使用情况下,“真理的谷物”在技术上是要求的,而“可实现”是一种技术便利。
Realizability is not totally necessary in order for Bayesian reasoning to make sense. If you think of a set of hypotheses as “experts”, and the current posterior probability as how much you “trust” each expert, then learning according to Bayes’ Law, \(P(h|e) = \frac{P(e|h) \cdot P(h)}{P(e)}\), ensures arelative bounded lossproperty.
Specifically, if you use a prior \(\pi\), the amount worse you are in comparison to each expert \(h\) is at most \(\log \pi(h)\), since you assign at least probability \(\pi(h) \cdot h(e)\) to seeing a sequence of evidence \(e\). Intuitively, \(\pi(h)\) is your initial trust in expert \(h\), and in each case where it is even a little bit more correct than you, you increase your trust accordingly. The way you do this ensures you assign an expert probability 1 and hence copy it precisely before you lose more than \(\log \pi(h)\) compared to it.
The prioraixi是based on is theSolomonoff prior。It is defined as the output of a universal Turing machine (UTM) whose inputs are coin-flips.
In other words, feed a UTM a random program. Normally, you’d think of a UTM as only being able to simulate deterministic machines. Here, however, the initial inputs can instruct the UTM to use the rest of the infinite input tape as a source of randomness to simulate a随机Turing machine.
Combining this with the previous idea about viewing Bayesian learning as a way of allocating “trust” to “experts” which meets a bounded loss condition, we can see the Solomonoff prior as a kind of ideal machine learning algorithm which can learn to act like any algorithm you might come up with, no matter how clever.
For this reason, we shouldn’tnecessarilythink of AIXI as “assuming the world is computable”, even though it reasons via a prior over computations. It’s getting bounded loss on its predictive accuracyas compared with任何可计算的预测指标。我们应该说AIXI假设所有可能的算法都是可计算的,而不是世界。
However, lacking realizability can cause trouble if you are looking for anything more than bounded-loss predictive accuracy:
- the posterior can oscillate forever;
- probabilities may not be calibrated;
- estimates of statistics such as the mean may be arbitrarily bad;
- estimates of latent variables may be bad;
- and the identification of causal structure may not work.
那么Aixi在没有实现性假设的情况下表现良好吗?我们不知道。尽管损失有限predictionswithout realizability, existing optimality results for itsactionsrequire an added realizability assumption.
首先,如果环境是sampled from the Solomonoff distribution, AIXI gets themaximum expected reward。但这是相当微不足道的。从本质上讲,这是Aixi的定义。
Second, if we modify AIXI to take somewhat randomized actions—Thompson sampling—there is anasymptoticoptimality resultfor environments which act like any stochastic Turing machine.
So, either way, realizability was assumed in order to prove anything. (See Jan Leike,Nonparametric General Reinforcement Learning。)
但是我指出的担心是not“世界可能是无法兼容的,因此我们不知道Aixi是否会做得很好”;这更多是一个说明性的情况。关注的是,Aixi只能通过构建代理来定义智力或理性much, much bigger比它必须学习和在内部采取行动的环境。
Laurent Orseau provides a way of thinking about this in “时空嵌入式智能”。但是,他的方法定义了代理商的智慧,从某种超级智能设计师来看,他从外部思考现实,选择代理商place into the environment。
Embedded agents don’t have the luxury of stepping outside of the universe to think about how to think. What we would like would be a theory of rational belief forsituated提供的基础与贝叶斯主义为二元代理提供的基础类似。
Imagine a computer science theory person who is having a disagreement with a programmer. The theory person is making use of an abstract model. The programmer is complaining that the abstract model isn’t something you would ever run, because it is computationally intractable. The theory person responds that the point isn’t to ever run it. Rather, the point is to understand some phenomenon which will also be relevant to more tractable things which you would want to run.
I bring this up in order to emphasize that my perspective is a lot more like the theory person’s. I’m not talking about AIXI to say “AIXI is an idealization you can’t run”. The answers to the puzzles I’m pointing at don’t need to run. I just want to understand some phenomena.
However, sometimes a thing that makes some theoretical models less tractable also makes that model too different from the phenomenon we’re interested in.
The方式aixiwins games is by assuming we can do true Bayesian updating over a hypothesis space, assuming the world is in our hypothesis space, etc. So it can tell us something about the aspect of realistic agency that’s approximately doing Bayesian updating over an approximately-good-enough hypothesis space. But embedded agents don’t just need approximate solutions to that problem; they need to solve several problems that aredifferent in kindfrom that problem.
One major obstacle a theory of embedded agency must deal with isself-reference。
Paradoxes of self-reference such as theliar paradoxmake it not just wildly impractical, but in a certain senseimpossible为了使经纪人的世界模型准确反映世界。
骗子悖论涉及句子“这句话不正确”的状态。如果是真的,那一定是错误的。如果不是真的,那一定是正确的。
The difficulty comes in part from trying to draw a map of a territory which includes the map itself.
如果世界对我们“静止”,这很好。但是由于地图在世界上,different maps create different worlds。
Suppose our goal is to make an accurate map of the final route of a road which is currently under construction. Suppose wealsoknow that the construction team will get to see our map, and that construction will proceed so as to disprove whatever map we make. This puts us in a liar-paradox-like situation.

Problems of this kind become relevant fordecision-making在游戏理论中。如果玩家试图获胜,那么一个简单的岩石剪裁游戏可以引入骗子悖论,并且可以互相预测比机会更好。
Game theory solves this type of problem with game-theoretic equilibria. But the problem ends up coming back in a different way.
我提到的现实性问题s on a different character in the context of game theory. In an ML setting, realizability is a potentiallyunrealisticassumption, but can usually be assumed consistently nonetheless.
In game theory, on the other hand, the assumption itself may be inconsistent. This is because games commonly yield paradoxes of self-reference.
Because there are so many agents, it is no longer possible in game theory to conveniently make an “agent” a thing which is larger than a world. So game theorists are forced to investigate notions of rational agency which can handle a large world.
不幸的是,这是通过将世界分为“代理”部分和“非代理”部分并以特殊方式处理代理来完成的。这几乎和代理的二元模型一样糟糕。
In rock-paper-scissors, the liar paradox is resolved by stipulating that each player play each move with \(1/3\) probability. If one player plays this way, then the other loses nothing by doing so. This way of introducing probabilistic play to resolve would-be paradoxes of game theory is called aNash equilibrium。
我们可以用纳什平衡防止assumption that the agents correctly understand the world they’re in from being inconsistent. However, that works just by telling the agents what the world looks like. What if we want to model agents who learn about the world, more like AIXI?
Thegrain of truth problem是the problem of formulating a reasonably bound prior probability distribution which would allow agents playing games to placesomepositive probability on each other’s true (probabilistic) behavior, without knowing it precisely from the start.
Until recently, known solutions to the problem were quite limited. Benja Fallenstein, Jessica Taylor, and Paul Christiano’s “Reflective Oracles: A Foundation for Classical Game Theory” provides a very general solution. For details, see “A Formal Solution to the Grain of Truth Problem” Jan Leike,Jessica Taylor和Benja Fallenstein。
You might think that stochastic Turing machines can represent Nash equilibria just fine.

But if you’re trying to produce Nash equilibriaas a result of reasoning about other agents, you’ll run into trouble. If each agent models the other’s computation and tries to run it to see what the other agent does, you’ve just got an infinite loop.
There are some questions Turing machines just can’t answer—in particular, questions about the behavior of Turing machines. The halting problem is the classic example.
Turing studied “oracle machines” to examine what would happen if we could answer such questions. An oracle is like a book containing some answers to questions which we were unable to answer before.
But ordinarily, we get ahierarchy。Type B machines can answer questions about whether type A machines halt, type C machines have the answers about types A and B, and so on, but no machines have answers about their own type.
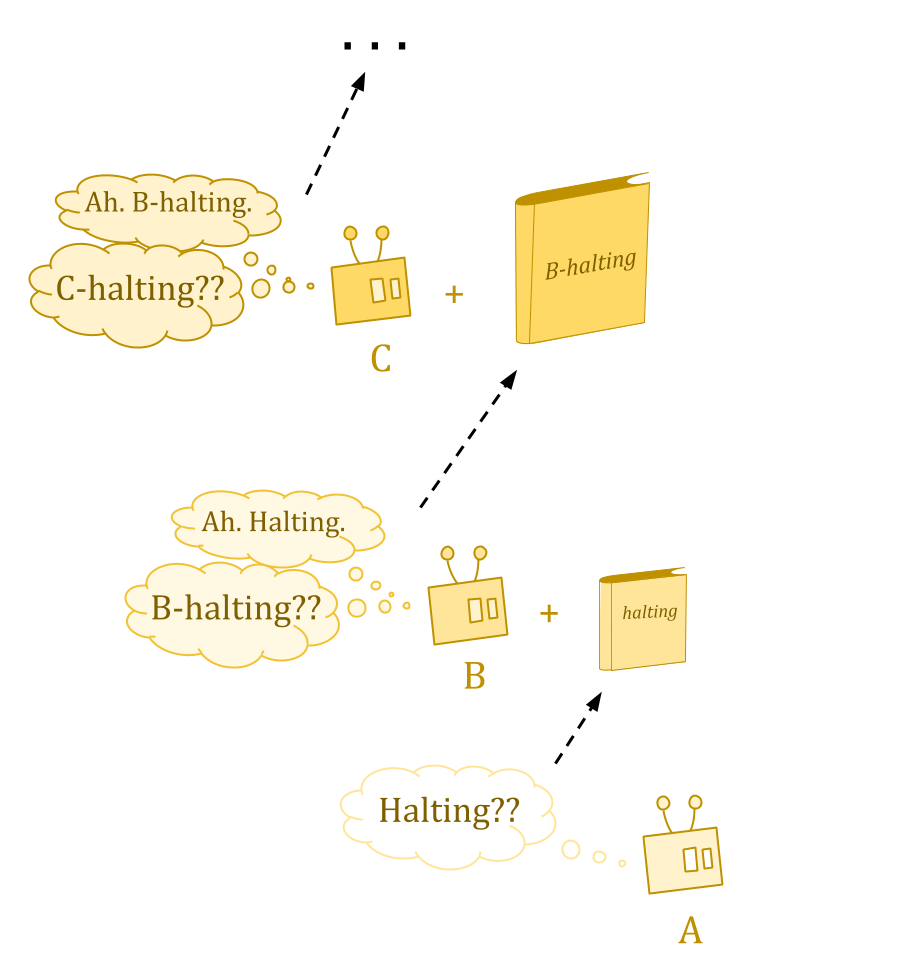
反光甲骨可以通过将普通的图灵宇宙扭转自身来起作用,因此,您可以定义一种用作自己的甲骨文机器的甲骨文,而不是无限的orace层。

这通常会引入矛盾,但是反射性的甲壳通过在偶然的悖论的情况下随机将其输出随机避免这种情况。所以反射性的甲骨文机器are随机, but they’re more powerful than regular stochastic Turing machines.
这就是反思性甲骨文解决我们前面提到的地图本身就是该领域一部分的问题:随机化。
反射性甲骨文s also solve the problem with game-theoretic notions of rationality I mentioned earlier. It allows agents to be reasoned about in the same manner as other parts of the environment, rather than treating them as a fundamentally special case. They’re all just computations-with-oracle-access.
However, models of rational agents based on reflective oracles still have several major limitations. One of these is that agents are required to have unlimited processing power, just like AIXI, and so are assumed to know all of the consequences of their own beliefs.
In fact, knowing all the consequences of your beliefs—a property known aslogical omniscience—turns out to be rather core to classical Bayesian rationality.
So far, I’ve been talking in a fairly naive way about the agent having beliefs about hypotheses, and the real world being or not being in the hypothesis space.
It isn’t really clear what any of that means.
Depending on how we define things, it may actually be quite possible for an agent to be smaller than the world and yet contain the right world-model—it might know the true physics and initial conditions, but only be capable of inferring their consequences very approximately.
人类肯定习惯于与速记和近似值一起生活。但是,这种情况可能是现实的,它可能与贝叶斯人知道某事的含义不符。贝叶斯人知道其所有信念的后果。
Uncertainty about the consequences of your beliefs islogical uncertainty。In this case, the agent might be empirically certain of a unique mathematical description pinpointing which universe she’s in, while being logically uncertain of most consequences of that description.
Modeling logical uncertainty requires us to have a combined theory of logic (reasoning about implications) and probability (degrees of belief).
Logic and probability theory are two great triumphs in the codification of rational thought. Logic provides the best tools for thinking aboutself-reference, while probability provides the best tools for thinking aboutdecision-making。However, the two don’t work together as well as one might think.
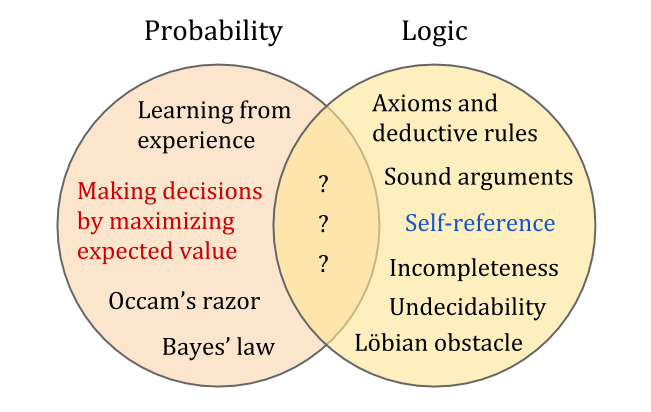
They may seem superficially compatible, since probability theory is an extension of Boolean logic. However, Gödel’s first incompleteness theorem shows that any sufficiently rich logical system is incomplete: not only does it fail to decide every sentence as true or false, but it also has no computable extension which manages to do so.
(See the post “一个不可流动的数学家插图” for more illustration of how this messes with probability theory.)
This also applies to probability distributions: no computable distribution can assign probabilities in a way that’s consistent with a sufficiently rich theory. This forces us to choose between using anuncomputable distribution, or using a distribution which is inconsistent.
Sounds like an easy choice, right? The inconsistent theory is at least computable, and we are after all trying to develop a theory of logicalnon-omniscience. We can just continue to update on facts which we prove, bringing us closer and closer to consistency.
Unfortunately, this doesn’t work out so well, for reasons which connect back to realizability. Remember that there arenocomputable probability distributions consistent with all consequences of sound theories. So our non-omniscient prior doesn’t even contain a single correcthypothesis。
This causes pathological behavior as we condition on more and more true mathematical beliefs. Beliefs wildly oscillate rather than approaching reasonable estimates.
Taking a Bayesian prior on mathematics, and updating on whatever we prove, does not seem to capture mathematical intuition and heuristic conjecture very well—unless we restrict the domain and craft a sensible prior.
概率就像一个量表,世界作为权重。观察结果消除了一些可能的世界,消除了权重并改变信念的平衡。
逻辑就像一棵树,根据推理规则从公理的种子生长。对于现实世界的代理人,增长过程永远不会完成。您永远不会知道每种信念的所有后果。
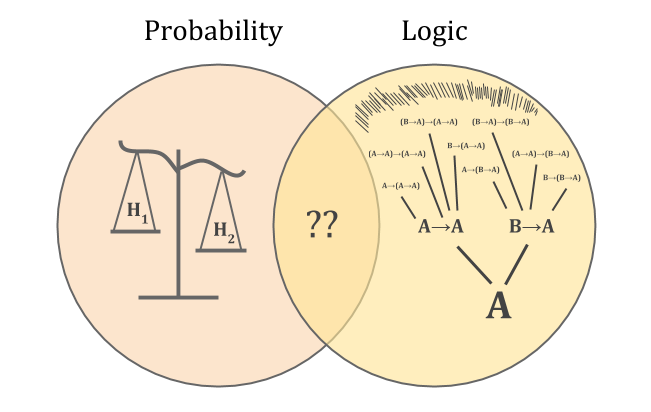
Without knowing how to combine the two, we can’t characterize reasoning probabilistically about math. But the “scale versus tree” problem also means that we don’t know how ordinary empirical reasoning works.
Bayesian hypothesis testing requires each hypothesis to clearly declare which probabilities it assigns to which observations. That way, you know how much to rescale the odds when you make an observation. If we don’t know the consequences of a belief, we don’t know how much credit to give it for making predictions.
这就像不知道将权重放在概率尺度上。我们可以尝试将重量放在两边,直到证明规则一体,但是这些信念只是永远振荡,而不是做任何有用的事情。
This forces us to grapple directly with the problem of a world that’s larger than the agent. We want some notion of boundedly rational beliefs about uncertain consequences; butany关于逻辑的可计算信念一定已经排除在外something, since the tree of logical implications will grow larger than any container.
For a Bayesian, the scales of probability are balanced in precisely such a way thatno Dutch bookcan be made against them—no sequence of bets that are a sure loss. But you can only account for all Dutch books if you know all the consequences of your beliefs. Absent that, someone who has explored other parts of the tree can Dutch-book you.
But human mathematicians don’t seem to run into any special difficulty in reasoning about mathematical uncertainty, any more than we do with empirical uncertainty. So what characterizes good reasoning under mathematical uncertainty, if not immunity to making bad bets?
One answer is to weaken the notion of Dutch books so that we only allow bets based onquickly computableparts of the tree. This is one of the ideas behind Garrabrant et al.’s “Logical Induction”, an early attempt at defining something like “Solomonoff induction, but for reasoning that incorporates mathematical uncertainty”.
Another consequence of the fact that the world is bigger than you is that you need to be able to usehigh-level world models:涉及桌子和椅子之类的模型。
This is related to the classical symbol grounding problem; but since we want a formal analysis which increases ourtrustin some system, the kind of model which interests us is somewhat different. This also relates to透明度andinformed oversight:世界模型应由可理解的部分制成。
A related question is how high-level reasoning and low-level reasoning relate to each other and to intermediate levels:multi-level world models。
标准的概率推理不提供very good account of this sort of thing. It’s as though you have different Bayes nets which describe the world at different levels of accuracy, and processing power limitations force you to mostly use the less accurate ones, so you have to decide how to jump to the more accurate as needed.
Additionally, the models at different levels don’t line up perfectly, so you have a problem of translating between them; and the models may have serious contradictions between them. This might be fine, since high-level models are understood to be approximations anyway, or it could signal a serious problem in the higher- or lower-level models, requiring their revision.
在ontological crises, in which objects we value turn out not to be a part of “better” models of the world.
它本身ems fair to say that everything humans value exists in high-level models only, which from a reductionistic perspective is “less real” than atoms and quarks. However,becauseour values aren’t defined on the low level, we are able to keep our values even when our knowledge of the low level radically shifts. (We would also like to be able to say something about what happens to values if thehighlevel radically shifts.)
Another critical aspect of embedded world models is that the agent itself must be in the model, since the agent seeks to understand the world, and the world cannot be fully separated from oneself. This opens the door to difficult problems ofself-referenceand人类决策理论。
Naturalized induction是the problem of learning world-models which include yourself in the environment. This is challenging because (as Caspar Oesterheldhas put it) there is a type mismatch between “mental stuff” and “physics stuff”.
aixiconceives of the environment as if it were made witha slot which the agent fits into。We might intuitively reason in this way, but we can also understand a physical perspective from which this looks like a bad model. We might imagine instead that the agent separately represents:self-knowledgeavailable to introspection; hypotheses about what the universe is like; and a “bridging hypothesis” connecting the two.
There are interesting questions of how this could work. There’s also the question of whether this is the right structure at all. It’s certainly not how I imagine babies learning.
Thomas Nagel会说解决问题的方式涉及“无处不在的观点”。每个假设都像从外面看一样,都像从外面看一样。这也许是一件奇怪的事情。
代理需要推理自己的特殊情况是代理需要推理自己的futureself。
To make long-term plans, agents need to be able to model how they’ll act in the future, and have a certain kind oftrustin their future goals and reasoning abilities. This includes trusting future selves that have learned and grown a great deal.
在传统的贝叶斯框架中,“学习”是指贝叶斯更新。但是正如我们指出的那样,贝叶斯更新要求代理商start outlarge enough to consider a bunch of ways the world can be, and learn by ruling some of these out.
Embedded agents needresource-limited,逻辑上不确定更新,这是不起作用的。
不幸的是,贝叶斯更新的主要方式e know how to think about an agent progressing through time as one unified agent. The Dutch book justification for Bayesian reasoning is basically saying this kind of updating is the only way to not have the agent’s actions on Monday work at cross purposes, at least a little, to the agent’s actions on Tuesday.
Embedded agents are non-Bayesian. And non-Bayesian agents tend to get into wars with their future selves.
Which brings us to our next set of problems:robust delegation。
This is part of Abram Demski and Scott Garrabrant’s嵌入式代理顺序。下一部分:Robust Delegation。
你喜欢这个帖子吗?You may enjoy our otherAnalysisposts, including: